LIMIT TRIGONOMETRI
Pengertian
Limit trigonometri adalah nilai terdekat suatu sudut pada fungsi trigonometri. Perhitungan limit fungsi trigonometri bisa langsung disubtitusikan seperti limit fungsi aljabar tetapi ada fungsi trigonometri yang harus diubah terlebih dahulu ke identitas trigonometri untuk limit tak tentu yaitu limit yang apabila kita langsung subtitusikan nilai nya bernilai 0, atau bisa juga untuk limit tak tentu tidak harus memakai identitas tetapi memakai teorema limit trigonometri dan ada juga yang memakai identitas dan teorema. Jadi, apabila suatu fungsi limit trigonometri di subtitusikan nilai yang paling mendekati nya menghasilkan dan maka kita harus menyelesaikan dengan cara lain.
Berbagai Macam – Macam Trigonometri dan Singkatannya
A. Macam – macam trigonometri
Berikut ini adalah nama – nama trigonometri yang biasa kita gunakan :
- Sinus ( sin )
- Tangen ( tan )
- Cosinus ( cos )
- Cotongen ( cot )
- Secan ( sec )
- Cosecan ( Csc )
B. Rumus kebalikan dalam trigonimetri
- sin∝ = 1/csc∝
- cos∝ = 1/sec∝
- tan∝ = 1/cot∝
- tan∝ = sin∝/cos∝
- cot∝=cos∝/sin∝
C. Identitas Trigonometri dalam trigonimetri
Sin2∝ + cos2∝ =1
1+cot2∝=csc2∝
Tan2∝+1=sec2∝
D. Rumus Jumlah dan Selisih dalam trigonimetri
E. Rumus Perkalian dalam trigonimetri
F. Rumus sudut rangkap dalam trigonimetri
Teorema Limit Trigonometri
Ada beberapa teorema yang dapat digunakan untuk menuntaskan persoalan limit trigonometri yaitu sebagai berikut :
Teorema A

Teorema tersebut hanya berlaku pada saat (x -> 0) .
Teorema B
Terdapat beberapa teorema yang berlaku. Untuk setiap bilangan real ( asli ) “c” di dalam daerah asal fungsi yaitu :
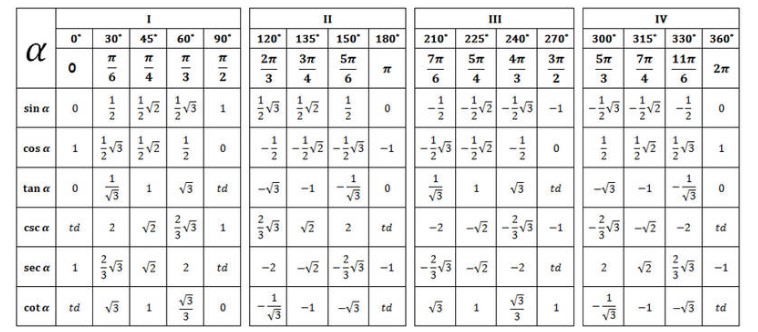
Biasanya dalam sebuah soal limit fungsi trigonometri nilai terdekat dari limit fungsi nya yaitu berupa sudut – sudut istimewa yaitu sudut yang mempunyai nilai sederhana. Karna itu kita perlu mengetahui nilai – nilai sudut istimewa yang terdapat pada tabel di bawah ini :
Tabel Sudut Istimewa
Rumus Limit Fungsi Trigonometri
Rumus-rumus diatas merupakan bekal atau prasyarat yang penting untuk digunakan dalam menghitung nilai limit trigonometri. Sebenarnya terdapat berbagai macam fungsi trigonometri yang sering muncul dalam permasalahan limit.
Pada pembahasan ini akan didiskusikan bagaimana menyelesaikan permasalahan limit fungsi trigonometri untuk x (atau variabel lainnya) mendekati nol. Sifat-sifat berikut kita gunakan untuk menyelesaikan permasalahan yang diberikan.
Contoh Soal Limit Fungsi Trigonometri
Hitunglah limit berikut :
Contoh Soal 1 :
Penyelesaian :
Jadi, limit fungsi trigonometri yang diberikan adalah 4.
Contoh Soal 2 :
Karena apabila kita langsung di subtitusikan menghasilkan 0 maka kita perlu menyelesaikan soal di tersebut dengan mengubahnya ke bentuk identitas.
Penyelesaian :
Contoh Soal 3 :
Penyelesaian :
Jadi, kita peroleh nilai limit fungsi yang diberikan adalah 2/9.
KONTINUITAS
Salah satu topik yang berkaitan dengan konsep limit fungsi adalah kekontinuan fungsi atau kontinuitas fungsi. Suatu fungsi dapat kontinu atau tidak kontinu di suatu titik.
Contoh Soal 1 :
Misalkan f suatu fungsi dari ℝ ke ℝ dengan aturan fungsi sebagai berikut.
Apakah f kontinu di x = 3?
Penyelesaian :
Limit kiri:
Limit kanan:
Ternyata nilai limit kirinya sama dengan limit kanannya, yaitu 4.
Kita simpulkan
dan
Langkah 2: Memeriksa apakah f terdefinisi di x = 3
Dari pendefinisian f, f(3) terdefinisi, yaitu f(3) = 2
Langkah 3: Memeriksa kesamaan nilai limit fungsi dengan nilai fungsinya
Dari langkah-langkah sebelumnya diperoleh bahwa
Kesimpulan: f tidak kontinu (atau diskontinu) di x = 3. Situasi pada contoh ini dapat dilihat pada dibawah ini.
Catatan:
Diskontinuitas di x = 3 pada Contoh 1 dinamakan ketidakkontinuan yang dapat dihapuskan. Dengan mendefinisikan kembali nilai f di x = 3, fungsi tersebut menjadi kontinu. Jadi, agar f kontinu di x = 3, kita definisikan f(3) = 4.
Contoh Soal 2 :
Misalkan g suatu fungsi dari ℝ ke ℝ dengan aturan fungsi sebagai berikut.
Apakah g kontinu di x = 0?
Penyelesaian :
Langkah 1: Memeriksa eksistensi limit fungsi di x = 0
Limit kiri:
Limit kanan:
Ternyata nilai limit kirinya tidak sama dengan limit kanannya, sehingga kita simpulkan:
tidak ada. Pada langkah ini juga, langsung simpulkan g tidak kontinu di x = 0. Situasi pada contoh ini dapat dilihat pada gambar dibawah ini.
Catatan:
Diskontinuitas di x = 0 pada Contoh 2 dinamakan ketidakkontinuan yang dapat tak terhapuskan. Kita tidak dapat mendefinisikan kembali nilai g di x = 0 untuk membuat g kontinu di sana.
Inilah pembahasan tentang rumus limit trigonimetri & kontinuitas beserta contoh soalnya, Semoga apa yang telah kita pelajari dalam artikel ini dapat bermanfaat serta menambah wawasan kita semua, khususnya untuk kasus seperti trigonometri & kontinuitas ini.






























Tidak ada komentar:
Posting Komentar