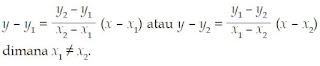FUNGSI
Pengertian Fungsi
Fungsi dalam matematika adalah suatu relasi yang menghubungkan setiap anggota x dalam suatu himpunan yang disebut daerah asal (Domain) dengan suatu nilai tunggal f(x) dari suatu himpunan kedua yang disebut daerah kawan (Kodomain).
Pada fungsi, terdapat beberapa istilah penting, di antaranya :
- Domain yaitu daerah asal fungsi f dilambangkan dengan Df.
- Kodomain yaitu daerah kawan fungsi f dilambangkan dengan Kf.
- Range yaitu daerah hasil yang merupakan himpunan bagian dari kodomain.
Range fungsi f dilambangkan dengan Rf.
Secara intuitif, y dapat dipandang sebagai fungsi dari x, jika terdapat aturan dimana nilai y (tunggal) menghubungkan nilai x.
Contoh :1. 𝒚 = 𝟐𝒙𝟐 + 𝟓
2. 𝒚 = 𝒙𝟐 − 𝟗
Definisi :
Suatu fungsi adalah suatu himpunan pasangan terurut (x,y) dimana himpunan semua nilai x disebut
daerah asal (domain) dan himpunan semua nilai y = f(x) disebut daerah hasil (ko-domain) dari fungsi.
(Notasi : f : A → B)
Untuk contoh 1, mendefinisikan suatu fungsi (namakan fungsi itu f). Fungsi f adalah himpunan pasangan terurut (x,y) sehingga x dan y memenuhi :
f = {(x,y) | 2x2 + 5}
x
|
0
|
1
|
-1
|
2
|
-2
|
…
|
10
|
y
|
5
|
7
|
7
|
13
|
13
|
…
|
205
|
Fungsi f ini memuat pasangan terurut (0,5); (1,7); (-1,7); (2,13); (-2,13); …; (10,205), dan f memuat tak berhingga banyak pasangan terurut.
Catatan :
1. Himpunan A,
B є ¡
2. Fungsi: y = f(x) ,
x
peubah
bebas
y
peubah
tak bebas, bergantung pada x
3. Daerah asal fungsi:
Df
= A = {x | fungsi f terdefinisi}
4. Daerah hasil fungsi: Wf = {y є B | y = f(x), x є Df }
Grafik
fungsi: {(x,y) | x є Df , y = f(x)) }
Ada
beberapa penyajian fungsi yaitu :
a. Secara verbal :
dengan uraian kata-kata.
b. Secara numerik : dengan tabel
c. Secara
visual : dengan
grafik
d. Secara aljabar : dengan
aturan/rumusan eksplisit
Contoh:
1. Secara
verbal
Biaya
pengiriman surat tercatat seberat w
ons adalah B(w). Aturan yang digunakan Kantor Pos adalah sebagai berikut. Biaya
pengiriman adalah Rp 1.000,00 untuk berat sampai satu ons, ditambah Rp 250,00
untuk setiap ons tambahan sampai 5 ons.
2. Secara numerik
Biaya
pengiriman surat tercatat ditunjukkan tabel berikut.
3. Secara
visual
Biaya
pengiriman surat tercatat ditunjukkan grafik berikut.
4. Secara
aljabar
Biaya
pengiriman surat tercatat dinyatakan oleh fungsi sebagai berikut.
JENIS-JENIS FUNGSI
SIFAT-SIFAT FUNGSI
1. Fungsi Into
Fungsi f : A → B disebut Into jika ada anggota B tidak mempunyai pasangan dengan anggota A.
2. Fungsi Onto ( Surjektif )
Fungsi f : A → B disebut onto jika setiap anggota B mempunyai pasangan anggota A. Sehingga berlaku f(a) = b. Dengan kata lain, suatu kodomain fungsi surjektif sama dengan kisarannya (range).
3. Fungsi Satu-Satu ( Injektif )
Misalkan fungsi f menyatakan A ke B maka fungsi f disebut suatu fungsi satu-satu (injektif), apabila setiap dua elemen yang berlainan di A akan dipetakan pada dua elemen yang berbeda di B. Selanjutnya secara singkat dapat dikatakan bahwa f : A→B adalah fungsi injektif . ( Untuk anggota B yang mempunyai pasangan dengan Anggota A, pasangan tersebut hanya satu ).
4. Fungsi Korespondensi Satu-satu ( Bijektif )
Fungsi f : A → B disebut korespondensi satu-satu jika fungsi tersebut injektif dan sekaligus surjektif.
GRAFIK FUNGSI
Diberikan
fungsi f. Himpunan {(x, y) : y = f (x), x Î D f } disebut grafik
fungsi f.
Menentukan Persamaan Garis Lurus
1. Menentukan Persamaan Garis yang Melalui Sebuah Titik (a,b) dengan Gradien m
Contoh Soal dan Pembahasannya
2. Menentukan Persamaan Garis yang Melalui Titik (x, y) dan (x, y)
Dengan menggunakan rumus pada bagian sebelumnya kalian akan peroleh persamaan garis berikut.
Contoh Soal dan Pembahasannya
3. Menentukan Persamaan Garis yang Sejajar Dengan Garis Lain dan Melalui Sebuah Titik
Contoh Soal dan Pembahasannya
4. Menentukan Persamaan Garis yang Tegak Lurus Dengan Garis Lain dan Melalui Sebuah Titik
Contoh Soal dan Pembahasannya
FUNGSI PANGKAT TIGA